We schetsen hier eerst even de problematiek. Eerst beperkte het rekenen zich tot tellen. Een voorbeeld hiervan vinden we in het Ishango-beentje, een kuitbeen van een baviaan met 168 inkepingen. Het vormt volgens onderzoekers één van de oudste voorbeelden van rekenhulpmiddelen. De groepering van de inkepingen is heel opvallend en doet vermoeden dat men gebruik maakte van een zes- en tiendelig talstelsel. Werd het staafje misschien gebruikt om te vermenigvuldigen? In de tentoonstelling zie je een 3D geprinte versie. Let op, het echte beentje dat je in het Koninklijk Belgisch Instituut voor Natuurwetenschappen in Brussel kan zien, is slechts 10 cm lang en heeft aan het uiteinde een kwartskristal. Het zou ca. 20.000 jaar oud zijn en is in 1950 gevonden in Congo.
In het grensgebied van Zuid-Afrika en Swaziland is een nog oudere rekenhulp gevonden, nl. het Lebombo beentje (ca. 43 000 jaar oud). Het heeft 29 inkepingen en deze refereren wellicht naar een maan(dstonden)cyclus.
Het aantal inkepingen is dus in dit geval een voorstelling van het getal 29. Maar zo'n voorstelling is om allerlei redenen niet zo handig. Stel je het getal 111 voor op deze manier, dan moet je al goed tellen om te weten te komen dat het om 111 gaat. Bovendien vraagt de voorstelling van het getal 111 met inkepingen ook al een eerder lang been.
Het was ook gebruikelijk getallen (of geld) voor te stellen door voorwerpen. Zo zijn bijvoorbeeld Kauri-schelpen tot begin/midden 19e eeuw gebruikt als munteenheid rond de Indische Oceaan.
Geleidelijk aan ontwikkelde zich de notie van een positietalstelsel, een systeem om getallen voor te stellen zoals ons tientallig stelsel waarbij de plaats van een cijfer bepaalt welke waarde ermee overeenkomt. In het tientallig stelsel kunnen we met 10 symbolen alle getallen voorstellen. Ons tientallig stelsel ontstond pas later. Vanaf ongeveer 10 000 voor Christus ontwikkelde zich in Azië een zestigtallig stelsel, waarbij de "cijfers" voorgesteld werden door objecten. Er was een object waarmee je "1" voorstelde, en een ander object dat "10" betekende, en weer een ander object voor "60". Geleidelijk aan ontstond dan het schrift, waarschijnlijk in Mesopotamië, bij de Sumeriërs, rond 3 200 voor Christus, en vanaf dan konden getallen in het zestigtallig stelsel ook opgeschreven worden.
De Sumeriërs gebruikten het zestigtallig stelsel voor hun astronomische berekeningen, maar voor het dagdagelijkse tellen werkten ze niet met basis 60 maar met basis 10. We vinden nog sporen terug van het gebruik van het zestigtallig stelsel in onze tijdsaanduidingen en in de voorstelling van hoeken m.b.v. (zestigdelige) graden.
Meer en meer raakte het rekenen in basis 10 en het positietalstelsel dat ermee overeenkwam, ingeburgerd. Maar het heeft nog een tijd geduurd voor de 10 symbolen die wij nu gebruiken om getallen voor te stellen, gemeengoed werden. Tot die tijd werd rekenen gedaan met abaci, waarbij het positietalstelsel met basis 10 gecombineerd werd met het voorstellen van cijfers m.b.v. een symbool of een object.
Het woord abacus (meervoud: abaci) komt uit het Latijn en betekent zandplaat. Dit Latijns woord vindt op zijn beurt z'n oorsprong in het Griekse abax (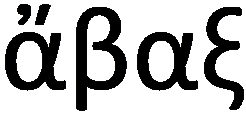
) en zou verwijzen naar een rechthoekig stuk materiaal. In het Arabisch betekent abq stof of zand. Het is dan ook niet verwonderlijk dat een heel populaire definitie een abacus omschrijft als "een bord bedekt met zand of stof" (waarin men kan schrijven en rekenen). De etymologische analyse doet enigszins vermoeden dat de eerste abaci bestonden uit een bord in bijvoorbeeld gedroogde klei of hout, bedekt met een laagje zand. Met een stok of een vinger konden symbolen in het zand worden voorgesteld. Door met het bord te schudden werd de berekening "gereset".
Nadien werd er gebruik gemaakt van kiezelsteentjes die in evenwijdige groeven werden gelegd op een stenen bord. In 1846 werd het zgn. Salamis bord (genoemd naar de vindplaats, nl. het eiland Salamis) gevonden. Dit is het oudste gekende rekenbord dat dateert van ongeveer 300 v.Chr. Het werd gebruikt door de Babyloniërs.
In de vroege Middeleeuwen maakte men in Europa vooral gebruik van een rekenbord/tafel en penningen. De Duitse wiskundige Adam Ries (1492-1559) beschrijft dit in zijn werk "Rechnung auff der linihen" (1518).
Een rekentafel is natuurlijk niet erg handig op verplaatsing. Dat zijn de verschillende "moderne" versies van abaci wel. In de tentoonstelling zijn verschillende types terug te vinden.
De Chinese abacus, de suanpan (
, "rekenblad") bestaat uit een rechthoekig kader. Daarin zitten minimaal zeven verticale staven (zie afbeelding verderop). Een horizontale balk maakt een scheiding tussen de bovenzijde waar meestal twee parels (kralen) per staaf zitten en de onderzijde met vijf parels per staaf (2:5 type). De parels in de onderste zone hebben de waarde 1 en deze in de bovenste zone de waarde 5. Door de parels naar de scheidingsbalk te schuiven worden ze in rekening gebracht. De parels in een Chinese abacus zijn meestal afgerond en vervaardigd uit hardhout of metaal.
De Japanse abacus, de soroban (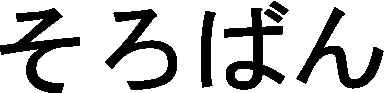
), is een "rekenbord" waarbij de parels dubbelkegelvormig zijn. De Chinese en Japanse abaci worden met de afrekenbalk horizontaal geplaatst.
Bij de Russische abacus, de schoty (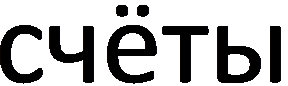
) is er geen afrekenbalk. Deze abacus wordt daarom ook verticaal geplaatst en enkel de kralen die tegen de linker kaderrand geschoven zijn, moeten in rekening gebracht worden.
Educatieve telramen bestaan er in verschillende vormen en uitvoeringen. Meestal hebben deze ook staven die horizontaal liggen, maar er bestaan er ook met gebogen staven.
De abacus werd veel gebruikt, en zelfs tot aan de Franse revolutie. Maar het was soms ook belangrijk om een berekening op papier te zetten. De Romeinse cijfers die sinds de oudheid gebruikt werden, waren alles behalve handig om mee te rekenen, en wel omdat het hier niet gaat over een positietalstel. Hoe vermenigvuldig je op een handige manier op papier XIII met IIXXX? Dat was niet mogelijk, dus werd er gezocht naar iets beters.
Soelaas kwam er in onze contreien uit Arabië, o.a. via Gerbert d'Aurillac, later paus Sylvester II, die rond het jaar 950 in het Westen een abacus introduceerde die gebruikmaakte van de Arabische cijfers zoals wij die nu kennen: 1, 2, 3, 4, 5, 6, 7, 8, 9. Nog geen 0, die kwam pas later. De 0 werd lange tijd niet als cijfer bekeken, maar was een plaatshouder: het getal 1031 schrijven als 1 31 bleek geen goed idee, daarom werd er op de plaats van het ontbrekende cijfer iets gezet om te laten zien dat er een lege plek was. De Arabische cijfers waren er dan al wel, maar voor het rekenen ermee zonder abacus was het wachten tot 1202, met het verschijnen van het boek Liber Abbaci van Leonardo van Pisa, bijgenaamd Fibonacci. De titel van dit boek doet verkeerdelijk vermoeden dat het gaat om een boek over abaci, maar dat is het niet. Het boek beschrijft hoe je kan rekenen met de Arabische cijfers:
Bron: http://www.museogalilei.it
Hier staat:
De negen Indische symbolen zijn 9 8 7 6 5 4 3 2 1. Met deze negen symbolen, en met het teken 0 dat de Arabieren zephyrus noemen, kan eender welk getal geschreven worden, zoals hieronder wordt getoond.
De invloed van dit boek is niet te onderschatten. Maar het heeft nog eeuwen geduurd voor de technieken die uitgelegd werden in het boek effectief gebruikt werden.
In 1494 verscheen het eerste grote boek over wiskunde: de Suma de Arithmetica Geometria Proportioni & Proportionalita van Luca Pacioli. In dat boek werden diezelfde technieken opnieuw uitgelegd, met een verwijzing naar het boek van Fibonacci. Geleidelijk aan begon men in het Westen te rekenen zoals wij dat nu nog doen.
Nu de cijfers er waren en ook de methodes om ermee te rekenen, kon er werk gemaakt worden van het mechaniseren van deze berekeningen!
Ishango-beentje, 3D-print in PLA
Deze replica is niet perfect op schaal en groter dan het origineel in het Koninklijk Belgisch Instituut voor Natuurwetenschappen in Brussel (ca. 100 mm). Het werd gemaakt door Arne Aerts op basis van een 3D-model van Paulafalcon op Sketchfab
Bron: https://sketchfab.com/3d-models/os-dishango-3840880170044c589b09afe4847986f8
Collectie: Universiteit Antwerpen
Kleine identieke voorwerpjes waren natuurlijk handig als munteenheid. In de landen rond de Indische Oceaan (Indië, Indonesië, Oost-Afrika en Oceanië) waren Kauri-schelpjes het gemeenschappelijke ruilmiddel bij uitstek. In Siam (het huidige Thailand) was een Kauri-schelpje 1/6400 baht waard. Een baht was equivalent met ongeveer 16 g zilver ofwel vandaag 12 euro. Een Kauri-schelpje is op die manier 0.2 eurocent waard. Deze doos schelpjes vertegenwoordigt dus niet bepaald een kapitaal.
Collectie: C. Vande Velde
De penningen vermelden de Franse zonnekoning en zijn voorganger in een tijdsbestek van 1610 (kroning Louis XIII) tot 1715 (dood van Louis XIV). In de 17e eeuw overheerste Nürnberg voor heel Europa de markt voor jetons, goedkoop geslagen en meestal van zeer dun metaal. Ze werden over heel Europa geëxporteerd en aangepast naar de smaak van het land van verkoop - vandaar: Franse koningen op Duitse rekenpenningen. Ze vermelden soms ook een belangrijke overwinning op het slagveld, gewoon “Jeton” of “rechenpfennig”, de naam van de maker, een beeltenis van een “rekenmeester”, of een stichtende spreuk (van GLVCK UND GLAS WIE BALD BRICHT DAS tot PIETATE ET IUSTITIA).
Collectie: C. Vande Velde
) – 2:5 typeDit metalen "rekenblad" heeft per staaf vijf kralen met een waarde "1" en twee kralen met een waarde "5". De meest rechtse staaf is voor de eenheid, links daarvan is voor de tientallen, enz. Enkel de kralen die tegen de horizontale balk geschoven zijn, hebben betekenis.
Collectie: E. Smet (item 303)
Chinese abacus (suanpan, ) – 2:5 type
Dit telraam heeft 42 (!) staven met telkens 5 kralen met een waarde "1" en 2 kralen met waarde "5". Let op de afgeronde vorm van de kralen bij een suanpan.
Collectie: E. Smet (item 356)
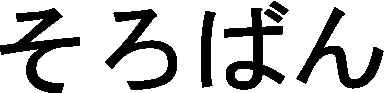) – 1:5 typeDit "rekenbord" of telraam is afgeleid van de Chinese suanpan. Ze heeft meestal een oneven aantal staven (9, 13, 21, 23, 27 of 31). Deze soroban heeft vijf zgn. aardkralen (kraal met waarde "1") en slechts één hemelkraal (kraal met waarde "5"). Tussen aard- en hemelkralen ligt de afrekenbalk.
Collectie: E. Smet (item 352)
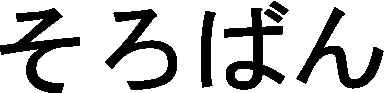) – 1:4 typeVanaf de jaren dertig van vorige eeuw werden ook de redundante aardkralen weggelaten. Vier aardkralen (kraal met waarde "1") en één hemelkraal (kraal met waarde "5") volstaan immers om te rekenen in het decimaal talstelsel.
Collectie: E. Smet (item 381)
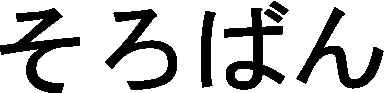) met "reset-knop" Bij het indrukken van de knop worden zowel de hemel- als de aardkralen van de afrekenbalk weggeduwd en dus op nul gezet.
Collectie: E. Smet (item 195)
)De staaf met vier kralen komt overeen met het decimale punt of kan gebruikt worden om met kwart-roebels te rekenen. De kleur van de meest linkse kraal van het duizendtal en het miljoental is rood.
Collectie: E. Smet (item 107)
)De staaf met vier kralen komt overeen met het decimale punt of kan gebruikt worden om met kwart-roebels te rekenen. De kleur van de meest linkse kraal van het duizendtal is zwart.
Collectie: E. Smet (item 237)
)"Fabriek voor huishoud chemicaliën" (Mozjaysk, Rusland), 1975-1979
Deze abacus heeft 1 roebel en 10 kopeke (1/100 roebel) gekost.
Collectie: E. Smet (item 366)
)Het aantal kralen van de onderste staaf is bij dit telraam ongewoon. Normaal zou men hier tien kralen verwachten met elk een waarde van één duizendste. Bij de oudere versies (van voor 1916) is het normaal dat er hier slechts vier kralen zijn met elk een waarde van één vierde kopeke. Waarom er in deze abacus zes kralen zijn, is niet duidelijk.
Collectie: E. Smet (item 106)
De Amerikaanse wiskundige Tim Cranmer ontwierp in 1962 deze abacus voor mensen met visuele beperkingen. De vilten achtergrond houdt de parels op hun plaats. Op de kader zijn uitspringende merktekens aangebracht.
Collectie: E. Smet (item 172)
Bij educatieve telramen beperkt men zich soms enkel tot een beperkt aantal (2, 3, ...) staven met 10 of 20 parels. Hiermee kunnen kinderen spelenderwijs hun eerste stappen zetten in de wondere rekenwereld.
Collectie: E. Smet (item 193, 325a, 326, 378) ?
