De directe aanleiding voor Wilhelm Schickard om zijn rekenklok te ontwikkelen was een ontmoeting met de wiskundige en astronoom Johannes Kepler (1571-1630)

Bronnen: portret Schickard: Roman Janssen; Oliver Auge (Hg.): Herrenberger Persönlichkeiten aus acht Jahrhunderten, Herrenberg 1999, ISBN 3-926809-09-4, p. 190; origineel in de Tübinger professorengalerij Conrad Melperger, Public domain, via Wikimedia Commons; rekenklok Schickard: Kepler, J., Caspar, M., van Dyck, W. Gesammelte Werke. Briefe 1620-1630, München, 1959; portret Kepler: August Köhler, Public domain, via Wikimedia Commons, Kepler Museum Weil-der-Stadt.
Kepler is vooral bekend door de Wetten van Kepler, drie wetten die de beweging van de planeten rond de zon beschrijven die o.a. door Isaac Newton zijn gebruikt om zijn zwaartekrachttheorie uit te werken. In het jaar 1600 kwam Kepler in contact met de astronoom Tycho Brahe die al een hele tijd bezig was met het noteren van de posities van de planeet Mars. Merk op dat er toen nog geen telescopen waren (uitvinding eerste telescoop: 1608) en dat deze waarnemingen met het blote oog moesten gebeuren. Brahe gebruikte daar enorme instrumenten voor om een goede nauwkeurigheid te krijgen. In de volgende figuur zie je bijvoorbeeld zijn muurkwadrant met een straal van 1.94 m.

Tycho Brahes muurkwadrant. Bron: waarschijnlijk uit de editie van 1598 van zijn Astronomiae instauratae mechanica, later met de hand ingekleurd.
Met de grote hoeveelheid erg nauwkeurige waarnemingen van Brahe van de posities van Mars slaagde Kepler er in om zijn drie wetten af te leiden. Hij had vijf jaar nodig om een wiskundig model op te stellen voor de baan van de planeet Mars. Van dit reusachtige werk zijn 987 pagina’s berekeningen (met de hand) bewaard gebleven.
In 1619, in een brief aan zijn vriend Vincenzo Bianchi, schrijft Kepler: Ik vraag jullie ook, mijn vrienden, me niet helemaal te veroordelen tot de tredmolen van wiskundige berekeningen, maar me tijd te laten om te besteden aan filosofische speculaties, mijn enige geneugten.
Kortom, erg graag deed hij dat rekenen niet. In dit kader is het belangrijk om te weten dat de decimale schrijfwijze van getallen nog niet echt ingeburgerd was op het ogenblik dat Kepler zijn berekeningen deed. Pas op het einde van de zestiende eeuw werd de notatie met het decimale punt ingevoerd, voordien werden getallen steeds geschreven als breuken met gehele teller en noemer. Bijvoorbeeld 3.1415 werd geschreven als:
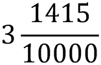
Het rekenen (optellen, aftrekken, delen, vermenigvuldigen) met zo’n breuken was helemaal niet eenvoudig. Daarom voerde Simon Stevin een nieuwe notatie in:
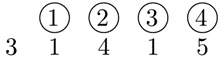
die dan uiteindelijk vervangen wordt door de gekende notatie 3.1415. Het eerste gebruik van het decimale punt dateert waarschijnlijk van 1593. Het kwam er dus eigenlijk op neer dat alle berekeningen in die tijd met de hand moesten gebeuren. In onderstaande figuur is een berekening te zien van de hand van Isaac Newton. In dit manuscript uit 1665 berekent hij de oppervlakte onder een hyperbool tot op 55 cijfers na de komma.

Bron: I. Newton, 1666, copyright Cambridge University Library, licensed under CCBY-NC 3.0)
In 1666 berekent Newton met de hand 16 decimalen van het getal π. Hij schrijft over deze berekening later, in een brief naar Henry Oldenburg: Pudet dicere ad quot figurarum loca has computationes otiosus eo tempore perduxi. Nam tunc sane nimis delectabar inventis hisce. Vrije vertaling: Ik ben beschaamd je te vertellen met hoeveel cijfers na de komma ik deze berekeningen heb gedaan. Ik had toen niet veel anders te doen, en genoot te erg van mijn eigen vondsten.

Bron: I. Newton, 1666, copyright Cambridge University Library, licensed under CCBY-NC 3.0)
De formule die Newton gebruikte bij zijn berekening was inderdaad een formule die hij zelf had gevonden.
Sommige wetenschappers maakten dankbaar gebruik van rekenwonders (mental calculators/calculateurs prodiges) om hen te helpen met hun rekenwerk. Het waren mensen die uiterst bedreven waren in het hoofdrekenen. In dezelfde brief van Kepler aan Bianchi klaagt hij tevens:
“Ik kan zelden een rekenaar voorzien. Ik heb Janus Gringalletus Sabaudus, een zeer ijverig rekenwonder, die alle wiskundige operaties beheerst, en die voor mij het werk van het berekenen van Ephemeriden voor vele jaren zou kunnen doen. Maar vermits ik, verlaten door de Keizer, hem niet kan voldoen, ben ik geenszins zeker van zijn aanwezigheid hier. En dan valt alles op mijn eigen schouders […] Soms vertraagt een misrekening, begaan in haast, me voor lange tijd.”
De wiskundige John Wallis was zelf een rekenwonder. Van hem wordt verteld dat hij slecht sliep en dan ’s nachts berekeningen deed in zijn hoofd. Een van die berekeningen was het trekken van een vierkantswortel uit een getal van 53 cijfers. De volgende ochtend dicteerde hij dan het uit 27 cijfers bestaande resultaat.
Vanaf 1614 was er een nieuw hulpmiddel beschikbaar dat het rekenen met decimale getallen sterk vereenvoudigde: de logaritmentafel. De Schotse wiskundige John Napier publiceerde in dat jaar zijn boek Mirifici Logarithmorum Canonis Descriptio (een beschrijving van de wonderbaarlijke canon van de logaritmen), dat behalve die beschrijving ook 90 pagina’s tabellen van goniometrische functies en hun logaritmen bevatte. Logaritmen waren ideaal als hulpmiddel bij vermenigvuldigingen en delingen, omdat deze door de logaritmische functie omgezet worden in optellingen en aftrekkingen.
Maar dat het met de hand allemaal toch niet zo snel vooruitging, dat zie je in de volgende tabel, die een korte geschiedenis bevat van de berekening van de decimalen van het getal π.
| (Aantal) decimalen | Wie? | Wanneer? | Hoe? |
|---|---|---|---|
| 3.14 | Ahmes (Rhind Papyrus) | 2000 v.C. | ? |
| 3.141 | Archimedes | Derde eeuw v.C. | Regelmatige 96-hoek |
| 3.141 | Ptolemaeus | Tweede eeuw | ? |
| 3.1415926 | Tsu Ch’ung Chi | Vijfde eeuw | 24675-hoek |
| 3.1415926535897932 (16 cijfers na het .) | Madhava of Sangamagrama (?) | 1400 | Reeks van Leibniz, versneld |
| 32 decimalen | Ludolph van Ceulen | 1600 | Met veelhoeken |
| 72 decimalen | Abraham Sharp | 1699 | Reeks van Gregory |
| 112 decimalen | Thomas Fantet de Lagny | 1719 | Reeks van Gregory |
| 136 decimalen | Baron Georg von Vega | 1794 | Reeks van Gregory |
| 200 decimalen | Zacharias Dase | 1844 | Boogtangensformule |
| 441 decimalen | William Rutherford en William Shanks | 1853 | Formule van Machin |
| William Shanks | 1874 | Formule van Machin | |
| 808 decimalen | D.F. Ferguson en John Wrench | 1947 | Formule van Machin |
| 1120 decimalen | L.B. Smith en John Wrench | 1949 | Formule van Machin |
| 2037 decimalen | E.N.I.A.C. (70 uur) | 1949 | Formule van Machin |
| 3089 decimalen | NORC (13 minuten) | 1953 | Formule van Machin |
Enkele aanvullingen bij de tabel:
In 1945 ontdekte D.F. Ferguson dat Shanks’ berekening vanaf decimaal 528 fout was, dus ook in de Salle Pi in Parijs. Deze fout werd daar (gelukkig) onmiddellijk gecorrigeerd. De van het plafond verwijderde getallen konden voor een groot deel gerecycleerd worden, want de lijst van 186 getallen bevat uiteraard grotendeels dezelfde getallen. Er waren vreemd genoeg na correctie wel 12 extra zevens nodig, en dan hebben we geen rekening gehouden met de tweekleurigheid van de cijfers!
