Wilhelm Schickard was inspired to develop his calculating clock after meeting the mathematician and astronomer Johannes Kepler (1571-1630).

Sources: portrait Schickard: Roman Janssen; Oliver Auge (Hg.): Herrenberger Persönlichkeiten aus acht Jahrhunderten, Herrenberg 1999, ISBN 3-926809-09-4, p. 190; original in the Tübinger Professorengalerij Conrad Melperger, Public domain, via Wikimedia Commons; Schickard calculating clock: Kepler, J., Caspar, M., van Dyck, W. Gesammelte Werke. Briefe 1620-1630, München, 1959; portrait Kepler: August Köhler, Public domain, via Wikimedia Commons, Kepler Museum Weil-der-Stadt.
Kepler is best known for Kepler's laws. These three laws describe the motion of the planets around the sun, and were used by Isaac Newton, among others, to derive his theory of gravity. In the year 1600, Kepler came into contact with the astronomer Tycho Brahe, who had been logging the positions of the planet Mars for a long time. As the telescope had not yet been invented (that came in 1608), these observations had to be made with the naked eye. To achieve good accuracy, Brahe used enormous instruments, such as the 1.94m wall quadrant shown in the figure below.

Tycho's Wall Quadrant: Tycho Brahe in his Uraniborg observatory on the island of Hven. Source: probably from the 1598 printing of his Astronomiae instauratae mechanica, later hand-coloured.
Using the wealth of data on the position of Mars collected by Brahe, Kepler was able to successfully derive his three laws. It took him five years to establish a mathematical model of the orbit of the planet Mars. Of this monumental feat, 987 pages of handwritten calculations have been preserved.
In a letter to his friend Vincenzo Bianchi in 1619, Kepler wrote: "I also ask you, my friends, not to condemn me to the treadmill of mathematical calculations, but to leave me the time to spend on philosophical speculations, my only joy."
In short, he was not a big fan of doing calculations. At the time, it was not yet common to use decimals in numeral notation; rather numbers were written as fractions with a whole nominator and denominator. Only at the end of the 16th century, the notation with a decimal point was conceived. For example, 3.1415 was written as:
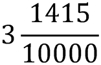
The challenges in performing calculations with fractions such as this one inspired Simon Stevin to introduce a new system of notation:
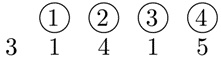
which eventually was replaced by the well-known notation 3.1415. The very first use of a decimal point likely dates to 1593.
To return to the question, why develop machines and other calculation aids? The answer boils down to the fact that until the end of the 16th century all calculations had to be done by hand. In the figure below, we see a calculation by the hand of Isaac Newton. The figure below shows a calculation done by Isaac Newton. In this manuscript from 1665, he calculated the area under a hyperbole to 55 decimal places.

Source: I. Newton, 1666, copyright Cambridge University Library, licensed under CCBY-NC 3.0)
In 1666, Newton calculated, by hand, the number π to 16 decimals. He later wrote about this calculation, in a letter to Henry Oldenburg:
Pudet dicere ad quot figurarum loca has computationes otiosus eo tempore perduxi. Nam tunc sane nimis delectabar inventis hisce.
Freely translated: "I am ashamed to tell you to what number of digits I have performed these calculations. I did not have much else to do, and enjoyed my findings too much."

Source: I. Newton, 1666, copyright Cambridge University Library, licensed under CCBY-NC 3.0)
The formula Newton used in his calculation was one he had discovered himself. Another method of calculation available to scientists at this time, was the use of mental calculators, or calculating prodigies (Fr: "calculateurs prodiges" German: "Rechenwunder"). These people were highly adept at performing mental arithmetic, and as such were hired to help the scientists with their tedious calculations. In the same letter from Kepler to Bianchi, he also complains:
“I can rarely provide for a calculator. I have Janus Gringalletus Sabaudus, a very apt calculating prodigy, who masters all mathematical operations, and who could do the work of calculating the Ephemerides for me for years. But seeing that I have been deserted by the Emperor, I cannot compensate him, and am by no means certain of his presence here. And then everything falls on my own shoulders [...] Sometimes a miscalculation, made in haste, delays me for a long time."
Mathematician John Wallis was a calculating prodigy himself. It is said that he slept very badly, and therefore did mental calculations at night. One of those calculations was calculating the square root of a 53 digit number. The next morning, he was able to dictate the 27 digit result from memory
As of 1614, a new aid was available that simplified calculation with decimal numbers: the logarithm table. The Scottish mathematician John Napier published his book Mirifici Logarithmorum Canonis Descriptio which contained not only a description of the "marvelous canon of logarithms", but also 90 pages of goniometric functions and their logarithms. Logarithms are an ideal aid for multiplication and division, because they convert these to addition and subtraction using the logarithmic function.
However, hand calculations were very time-consuming, as shown in the following table, which gives a brief history of the calculation of the decimals of the number π.
| (Number of) decimals | Who? | When? | How? |
|---|---|---|---|
| 3.14 | Ahmes (Rhind Papyrus) | 2000 B.C. | ? |
| 3.141 | Archimedes | Third century B.C. | Regular 96-gon |
| 3.141 | Ptolemaeus | Second century | ? |
| 3.1415926 | Tsu Ch’ung Chi | Fifth century | 24675-gon |
| 3.1415926535897932 (16 after the .) | Madhava of Sangamagrama (?) | 1400 | Series of Leibniz, accelerated |
| 32 decimals | Ludolph van Ceulen | 1600 | with polygons |
| 72 decimals | Abraham Sharp | 1699 | Series of Gregory |
| 112 decimals | Thomas Fantet de Lagny | 1719 | Series of Gregory |
| 136 decimals | Baron Georg von Vega | 1794 | Series of Gregory |
| 200 decimals | Zacharias Dase | 1844 | Arctan formula |
| 441 decimals | William Rutherford and William Shanks | 1853 | Machin's formula |
| William Shanks | 1874 | Machin's formula | |
| 808 decimals | D.F. Ferguson and John Wrench | 1947 | Machin's formula |
| 1120 decimals | L.B. Smith and John Wrench | 1949 | Machin's formula |
| 2037 decimals | E.N.I.A.C. (70 hours) | 1949 | Machin's formula |
| 3089 decimals | NORC (13 minutes) | 1953 | Machin's formula |
Some additions to the table:
In 1945, D.F. Ferguson discovered an error in Shanks’s calculation, starting at the 528th decimal. This discovery also meant that the digits in the Salle Pi in Paris were incorrect. Fortunately, this error could be quickly corrected by removing and reusing most numbers, because the list of 186 “new” decimals contained largely the same quantities of each digit. Strangely, 12 additional 7's were needed, and the numbers also occur in two different colors, which complicated matters further.
