Let us first outline the problem. At first, calculation was limited to counting. An example of this is the Ishango Bone, a baboon calf bone with 168 carved notches and, according to researchers, one of the oldest known arithmetic tools. The grouping of the notches is striking and suggests the use of a numbering system in bases six and ten. Perhaps the bone was used for multiplication? A 3D printed version is on display in the exhibition. Note that the real bone, on display at the Royal Belgian Institute of Natural History in Brussels, is only 10 cm long and has a quartz crystal embedded in one end. It is said to be 20,000 years old and was found in Congo in 1950.
In the border region between South Africa and Swaziland, an even older calculating aid was found, the Lemombo bone (ca. 43.000 years old). It has 29 notches, which may refer to a lunar/period cycle.
The number of notches is a representation of the number 29. But such a representation is not very practical for several reasons. If you imagine the number 111 in this way, you would have to be very good at counting to know that the number is 111. Also, representing 111 with notches requires a rather long bone.
It became common to represent numbers (or money) with objects. For example, cowrie shells were used as currency in countries around the Indian Ocean until the mid-19th century.
Gradually the idea of a positional numbering system was conceived, a way of representing numbers like our decimal system, where the position of a digit determines what value it represents. In the decimal system, we can represent all numbers using just 10 symbols. But our decimal system only came later. From about 10,000 BC, a system in base 60 was developed in Asia, where the digits were represented by objects. There was one object for "1", another for "10" and another for "60". Gradually, writing developed, probably in Mesopotamia, with the Sumerians, around 3200 BC, and from then on these numbers in base 60 could also be written down.
The Sumerians used base 60 for their astronomical calculations, but for everyday calculations, they used base 10 instead of base 60. We still find traces of the use of base 60 in our representation of time and of angles in (60-fold) degrees.
More and more calculations were done in base 10, and the corresponding positional system became common. But it took a while before the 10 symbols we use today came into general use. Until then, calculations were mainly done using the abacus, which combined the base 10 positional system with the representation of digits by a symbol or object.
The word abacus (plural abaci) originates from Latin and means "sand plate". The Latin word in turn finds its origin in the Greek abax (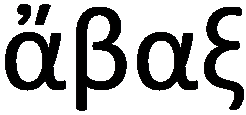
) and would refer to a rectangular piece of material. In Arabic, "abq" means "sand" or "dust". It is not surprising, then, that a popular definition describes an abacus as a "plate covered with sand or dust" (on which one can write and calculate). Etymological analysis suggests that the first abaci consisted of a board of dried clay or wood, covered with a layer of sand. Symbols could be drawn with a stick or a finger. By shaking the board, the calculation was "reset".
Later, use was made of pebbles, laid into parallel grooves in a stone board. In 1846, the so-called Salamis board was found (named after the place where it was found, the island of Salamis). This is the oldest known calculating board, dating from around 300 B.C. and used by the Babylonians.
In the early Middle Ages, in Europe mainly a calculating board/table was used with calculating tokens. The German mathematician Adam Ries (1492-1559) describes this in his work “Rechnung auff der linihen” (1518).
A calculating table is of course not very practical for travelling (although it is thought that there were textile versions that could be rolled up). Various modern versions of the abacus are much more portable. Several types are on display in the exhibition.
The Chinese abacus, the suanpan (
, "calculating board”) consists of a rectangular frame. There are at least seven vertical bars in this frame (see Figure 1). A horizontal bar divides the top (where there are usually two beads (or pearls)) and the bottom, with five beads per bar (2:5 type). The beads in the lower zone have value 1, those in the upper zone have value 5. By moving the beads to the centre bar, they are taken into account. The beads in a Chinese abacus are usually rounded and made of hardwood or metal.
The Japanese abacus, or soroban (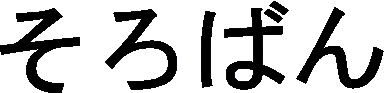
), is a "calculating board" in which the beads are bicone shaped. The Chinese and Japanese abacus are placed with the central bar horizontally.
The Russian abacus, the schoty (
) does not have a cetral bar. This abacus is placed vertically, and only the beads shifted to the left frame rail are taken into account.
Educational abaci come in many shapes and forms. Most have horizontal bars, but also examples with curved rods exist.
The abacus was widely used until the French Revolution. But sometimes it was also important to get a calculation on paper. Roman numerals, used since ancient times, were not very useful for calculations because they were not positional. How would you multiply XIII by IIXXX on paper? It was not easy (although there are tricks), so another solution was sought.
Solace came to our regions from Arabia via Gerbert d'Aurillac, later Pope Silvester II, who introduced an abacus to the West around 950, using the Arabic numerals we still know today: 1, 2, 3, 4, 5, 6, 7, 8, 9. No 0 yet, that came later. For a long time, 0 was not considered a number but a placeholder. Writing the number 1031 as 1 31 did not turn out to be a good idea, so instead of the "missing" number, "something" was written to indicate that a place was empty. So while Arabic numerals were around, we had to wait until 1202 for them to be used in calculations, with the publication of the “Liber Abaci” by Leonardo of Pisa, nicknamed Fibonacci. The title of the book misleadingly suggests that it is about abaci, but it isn't. Instead, it describes how to calculate with Arabic numbers:
Bron: http://www.museogalilei.it
This part reads:
The nine Indian symbols are 9 8 7 6 5 4 3 2 1. With these nine symbols, and the character 0, which the Arabs call Zephyrus, any number can be written, as demonstrated here below.
The influence of this book should not be underestimated. However, it took centuries before the techniques explained in the book were effectively used.
In 1494 the first great book on mathematics appeared - de Suma de Arithmetica Geometria Proportioni & Proportionalita by Luca Pacioli. In this book, the same techniques were explained again, with reference to Fibonacci's book. Gradually, people in the West began to calculate in the way we still do today.
Now the numbers were there, as well as the methods to calculate with them, so we could move on to mechanising these calculations!
Ishango-bone, 3D-print in PLA
This replica is not perfectly to scale, and larger than the original in the Royal Belgian Institute of Natural Sciences in Brussels (approx. 100mm). This replica was printed by Arne Aerts from a 3D model by Paulafalcon on Sketchfab
Source: https://sketchfab.com/3d-models/os-dishango-3840880170044c589b09afe4847986f8
Collection: University of Antwerp
Small identical objects were also useful as currency. In the countries around the Indian Ocean (India, Indonesia, East Africa and Oceania) cowrie shells were the common trade currency of choice. In Siam (modern Thailand) a cowrie shell was worth 1/6400 of a baht. One baht was equivalent to about 16g of silver, which is equivalent to 12 EUR today. Thus, one cowrie would be worth 0.2 cents. So this box is not exactly worth a fortune!
Collection: C. Vande Velde
The tokens refer to the French Sun King and his predecessor, in a period from 1610 (coronation of Louis XIII) to 1715 (death of Louis XIV). In the 17th century, Nürnberg dominated the market for calculating tokens. They were cheaply mass-produced from very thin metal and exported all over Europe, adapted to the taste of the destination - hence: French kings on German tokens. Sometimes they also mention an important victory, just “Jeton” or “Rechenpfennig”, the name of the maker, an image of a “calculating master” or an edifying saying (from GLVCK UND GLAS WIE BALD BRICHT DAS, to PIETATE ET IUSTITIA).
Collectie: C. Vande Velde
) – 2:5 typeThis metal "calculating board" has five pearls per rod with value "1" and two pearls with value "5". The rightmost rod is for units, the one to the left of that for tens, etc. Only the pearls moved to the middle division count.
Collection: E. Smet (item 303)
Chinese abacus (suanpan, ) – 2:5 type
This abacus has 42 (!) rods with always 5 pearls with value "1" and 2 with value "5". Notice the rounded shape of the pearls in a suanpan.
Collection: E. Smet (item 356)
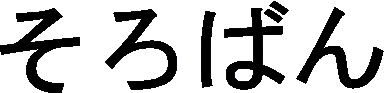) – 1:5 typeThis calculating or counting board is derived from the Chinese suanpan. It usually has an odd number of rods (9, 13, 21, 23, 27 of 31). This soroban has five so called earth pearls (value “1”) and one heaven pearl (value "5"). Between heaven and earth is the divider.
Collection: E. Smet (item 352)
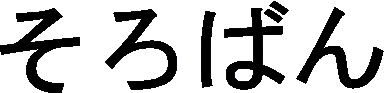) – 1:4 typeStarting in the 1930s, redundant pearls were omitted. Four earth pearls (value "1") and one heaven pearl (value "5") are sufficient to calculate in base 10.
Collection: E. Smet (item 381)
) with “reset” button Pressing the button pushes both heaven and earth pearls away from the centre divider, resetting the soroban to 0.
Collection: E. Smet (item 195)
)The rod with four pearls corresponds to the decimal point, or can be used to calculate with quarters of a ruble. The colour of the leftmost pearls of the thousand and million rods is red.
Collection: E. Smet (item 107)
)The rod with four pearls corresponds to the decimal point, or can be used to calculate with quarters of a ruble. The colour of the leftmost pearls of the thousands rod is black.
Collection: E. Smet (item 237)
)“Factory for household chemicals” (Mozjaysk, Russia), 1975-1979
This abacus cost 1 ruble and 10 kopeke (100ths of a ruble).
Collectie: E. Smet (item 366)
)The number of pearls on the lower rod of this abacus is unusual. Normally, one would expect 10 beads, each with a value of one 1000th. In older versions (pre-1916), it is normal to have only 4 pearls, each worth a quarter kopeke. Why there are 6 pearls in this abacus is unclear.
Collection: E. Smet (item 106)
The American mathematician Tim Cranmer designed this abacus in 1962, for the visually impaired. The felt base holds the beads in place. The frame has raised marks.
Collection: E. Smet (item 172)
Educational abaci are often made with a limited number of rods (2, 3, ...) and 10 or 20 beads. This is a fun way for children to take their first steps in the wonderful world of arithmetic.
Collection: E. Smet (item 193, 325a, 326, 378) ?
