This part of the exhibition outlines other developments in mechanical calculation from the 17th to the 19th centuries, starting with John Napier of Merchiston, a Scottish landowner, scientist, engineer and mathematician, who published the principles behind and the use of logarithms in 1614. They allow to convert a multiplication to an addition, which is of course a much simpler operation. Probably to facilitate the calculation of logarithms, he also specialised in calculation systems.
The famous "Napier's Bones", are a kind of dissected multiplication tables, that allow to calculate intermediate products mentally, with a minimum of writing. In 1623, Schickard was well aware of Napier's Bones, and implemented their use in the top part of his machine.
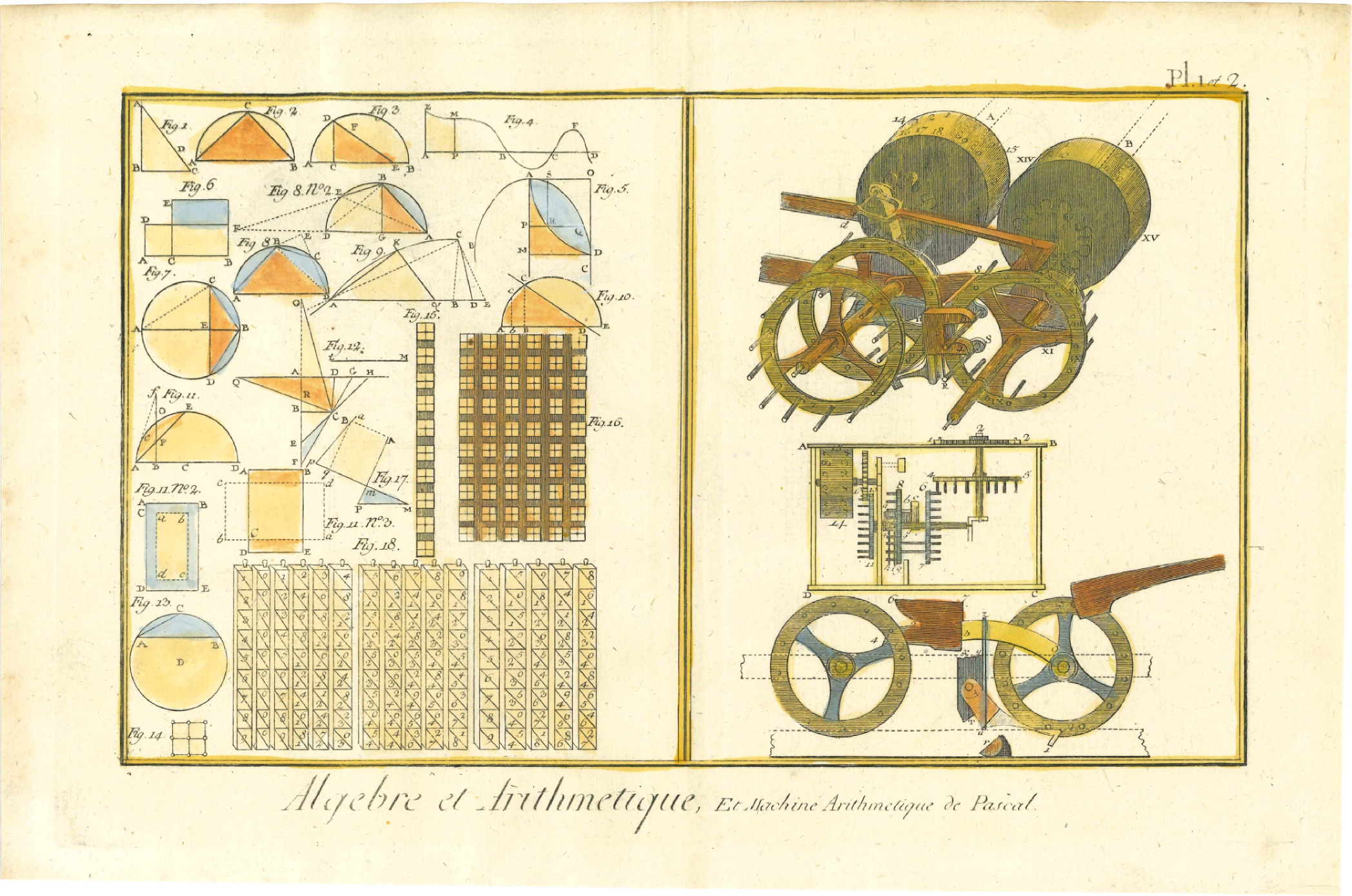
Blaise Pascal in France in 1642 developed a calculating machine that could add (and subtract using complementary numbers), but easy multiplication or division remained out of reach.
Gottfried Wilhelm Leibniz on the other hand, applied his "invention strategy" to mechanical calculation, and, in 1694, invented a machine where the number that is entered is not processed directly, but held independently during a calculation cycle. Combined with the mobility of the inscribed number with respect to the result register, this led to a true four-function calculator, including also multiplication and division. Later in the 17th, 18th and 19th centuries, several other people developed calculating machines based on various and diverse principles - among others the machines of Hahn, Müller, Braun, Vayringe, ... Calculating machines, until the 2nd half of the 19th century, were rather mechanical curiosities that found their place in the curiosity cabinets of the ruling class and monarchies, rather than being used in practice. As a result, they were often richly decorated, but not always so economically successful.
The man in the street remained condemned to mental arithmetic, used an abacus or calculating table, calculated longhand on paper, or used books of tables, which improved considerably throughout the years, sometimes also through the use of machines.
3D print in PLA (Napier's Bones - Manual Calculator, Gyrobot, https://www.thingiverse.com/thing:183676 )
A few months after the death of the eccentic Scottish scientist and nobleman John Napier (1550-1617), the book “Rabdologiae” appeared, in which he described his calculating rods. The square rods, made of ivory, bone or hardwood and inscribed with the multiplication tables, allowed rapid mental multiplication with a minimum of writing.

Collection: E. Smet (item 379)

Edal Anton Lefterov, CC BY-SA 3.0

uploader was Hajotthu at de.wikipedia, BY 3.0, via Wikimedia Commons

Source: wikimedia, CC BY-SA 3.0 FR, author: Rama
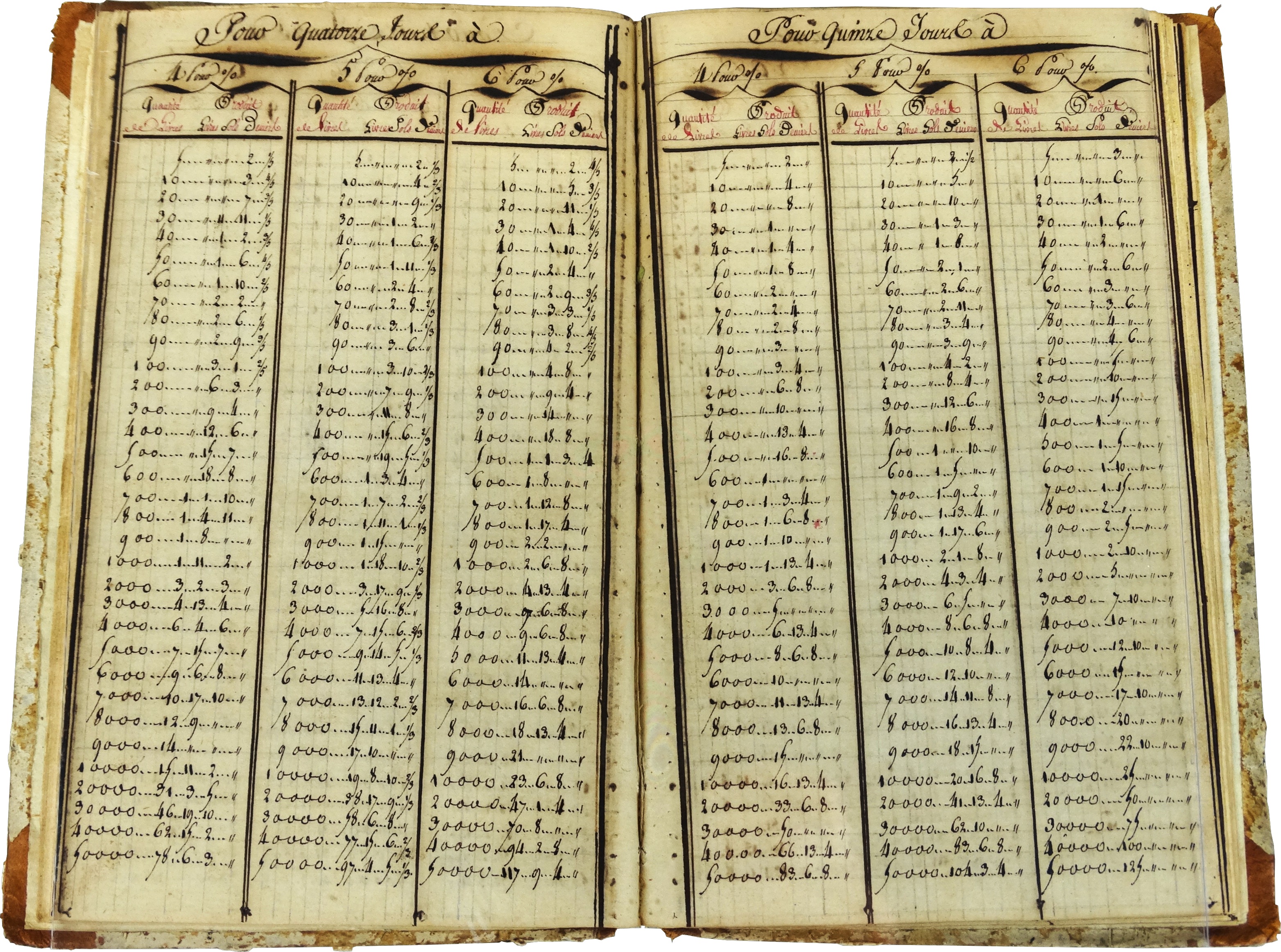
This handwritten booklet contains interest tables for the pre-revolutionary French monetary system. It allowed one to look up without calculation (or error) how much compound interest the customer would owe on a loan over a given period of time.
Tables were a necessary tool to be able to quickly find the values of difficult to calculate quantities, such as interests, goniometric functions or logarithms. The tables were created by a small army of human "computers", arranged on different levels according to their training, from expert mathematicians that selected the methods to the lowest level, where only interpolations were done between table values. De Prony, for calculating his tables, used 60-80 hairdressers that were out of work after the French revolution - a creative use of talent! (see “The history of Mathematical Tables – from Sumer to Spreadsheets”, ed. M. Campbell-Kelly, Oxford University Press, 2003)
Collection: C. Vande Velde
BELGISCHE NEGOCIANT, printing house Snoeck-Ducaju and son (Ghent), ca. 1830
These compact tables for merchants contain the exchange rates for various older currencies (e.g. "Belgian money - cents in Dutch and Brabant current money", "Gulders Dutch in Belgian", etc.), conversion tables for measures and weights (Belgian metres in Ghent raw linen feet), interest tables and a "Pythagorean table" of multiplication. The date of publication is not mentioned, but more recent editions exist under the title “Nieuwe Belgische Negociant”.

Collection: E. Smet (item 373)
SHERWIN’s Mathematical Tables, London, 1706 … 1771
There are several editions of Sherwin's popular book of tables (1706, 1710, 1717, 1726, 1742, 1761, 1771, 1785). Unfortunately, the title page of this book is missing, but we have been able to establish that this is the 1742 edition. Although the "reviewer" was promised a compensation if an error could be found in the tables, this was by no means a guarantee that the number of errors would decrease in later editions.

Collection: E. Smet (item 383)
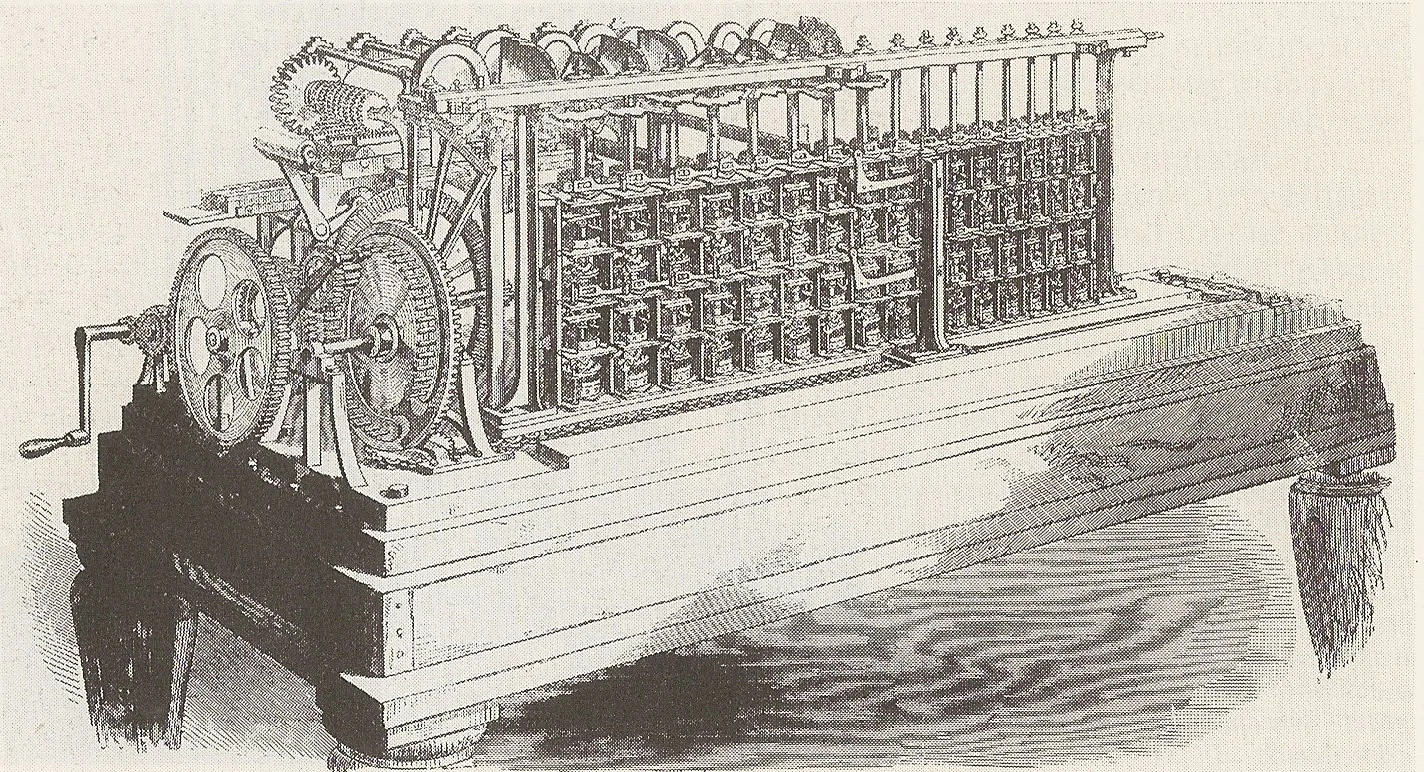
In the 19th century the formulae for calculating goniometric numbers and logarithms were implemented in "difference engines", the most famous (but not very successful) example being Charles Babbage's difference engine. These machines printed their results directly as an impression in a soft material, such as lead, plaster or papier-mâché, so that printing plates could be cast directly from the output, which could be published as a facsimile in book form, thus at least avoiding setting errors. This engraving from a magazine (Illustrated London News, June 30th 1855) shows the Scheutz's difference engine, which, much to the chagrin of Thomas de Colmar, received the gold medal at the London Exhibition 1855, instead of Thomas's piano arithmometer.
Collection: C. Vande Velde
This book of logarithmic tables is printed directly from the output of the Wiberg difference mechanism. Wiberg developed this machine in 1877, and unlike the machines of Babbage and Scheutz, it is only the size of a sewing machine, although the functionality is essentially the same. The machine itself is in the Tekniska Museet in Stockholm. The tables are (hopefully!) faultless - a great improvement!


Collection: C. Vande Velde